frechet.xyz

More applied than theory…

The Fréchet Distance

Similarity between curves

Started with (Alt and Godau 1995)

• Quadratic time / complicated (use parametric search)

• Large amount of work on extensions, implementation, etc.

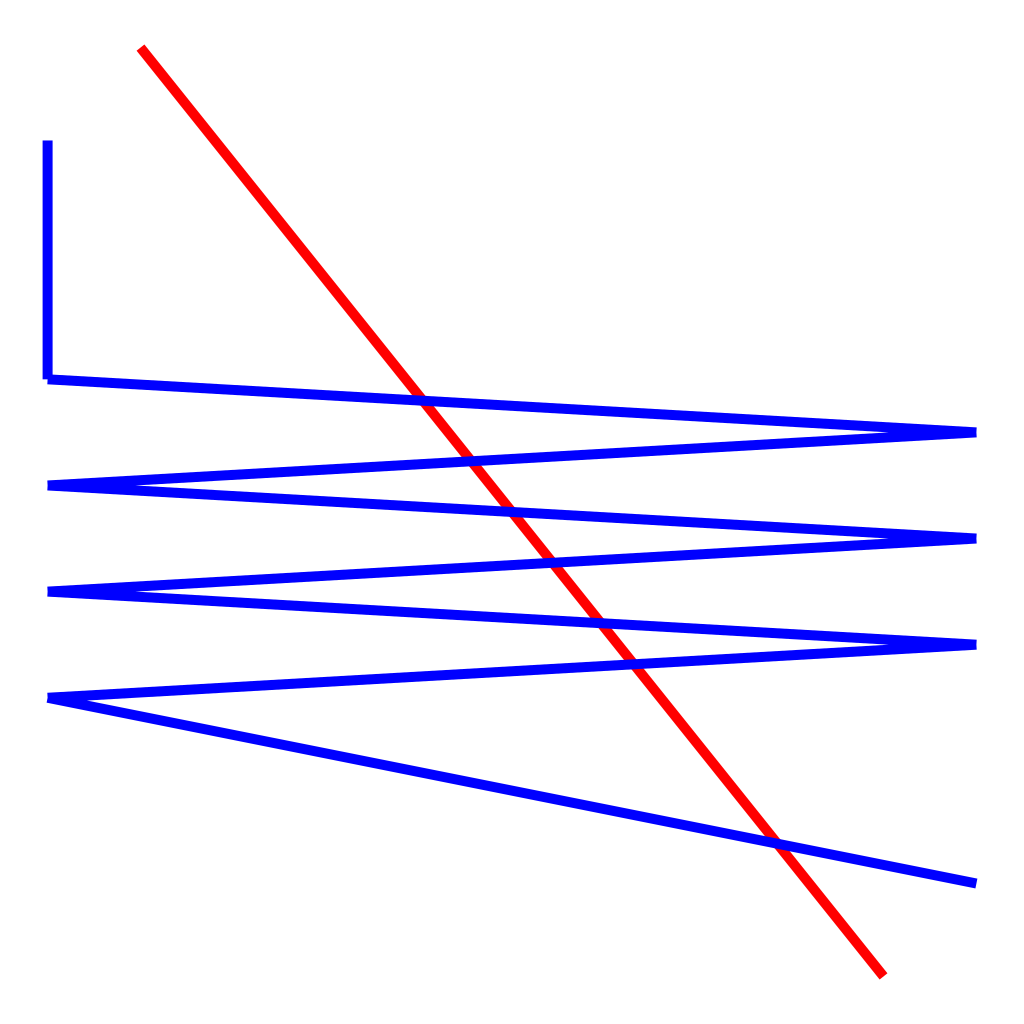
Frogs taking a walk

The Discrete Fréchet Distance

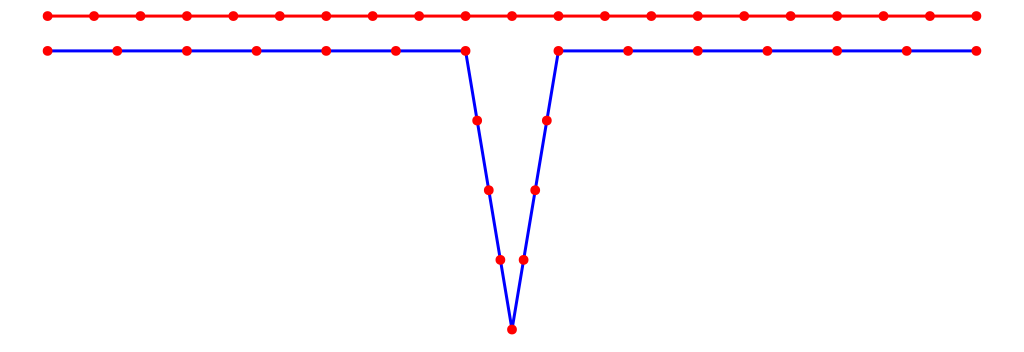
The problem

with the Fréchet Distance

The problem II

with the Fréchet Distance

This work

• More nuanced def of Fréchet Distance
• Better + simpler algorithms.
• Implementation (packages)
  • Julia https://github.com/sarielhp/FrechetDist.jl
  • Python https://github.com/eliotwrobson/FrechetLib
• Official packages
• New ideas from implementation.

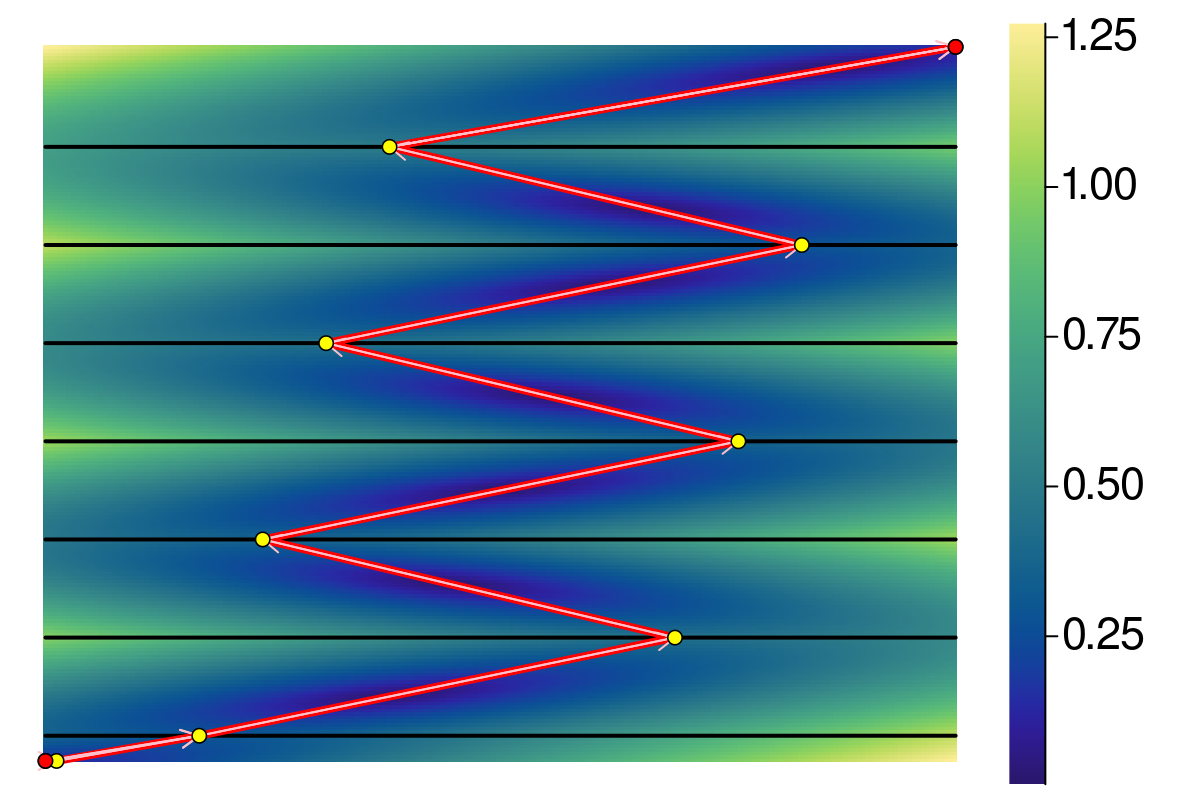
The Fréchet distance via free space diagram

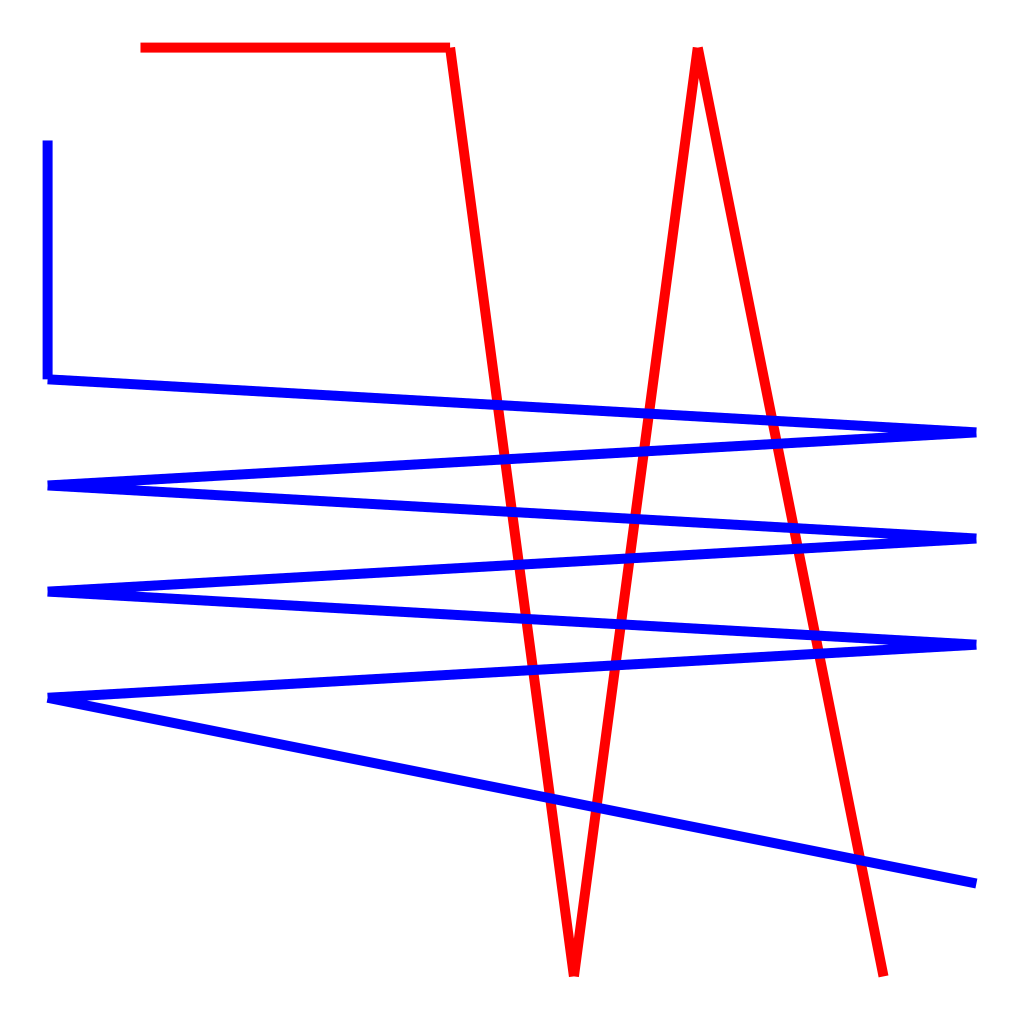
Fréchet distance: Free space diagram II

The Fréchet morphing in this case

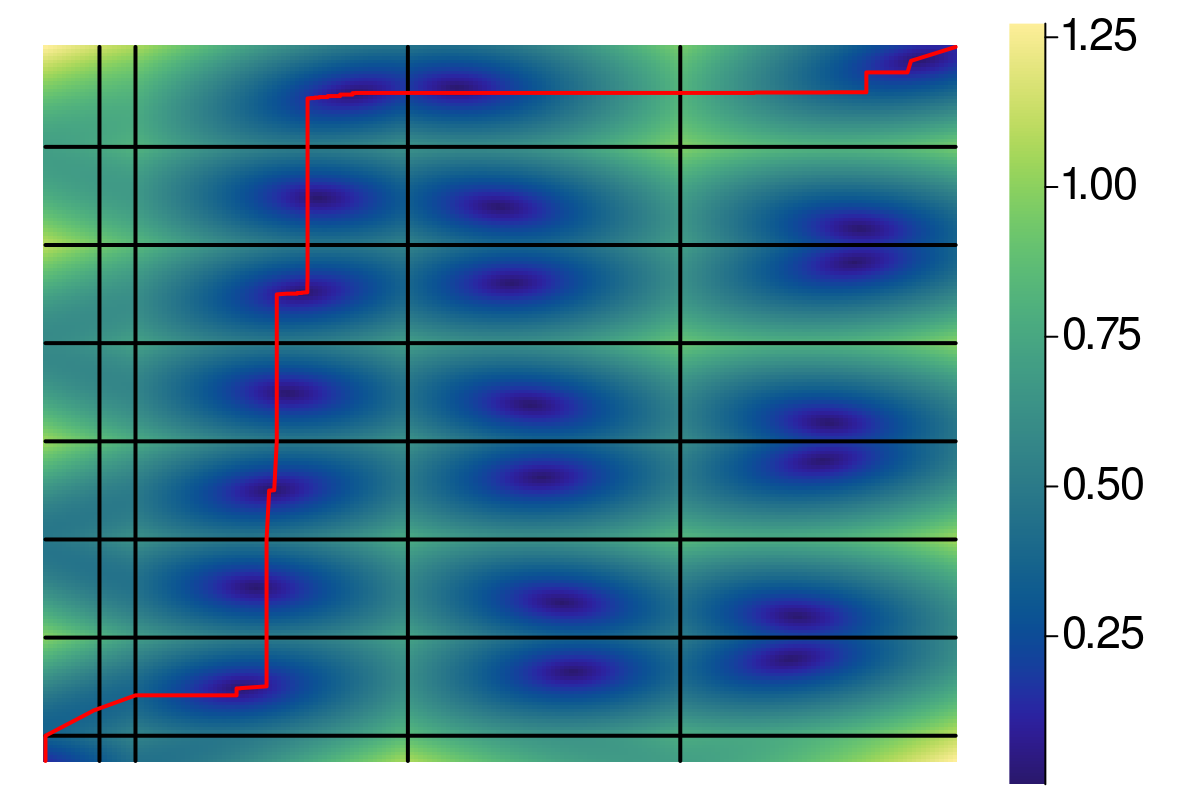
First idea: Make moves locally

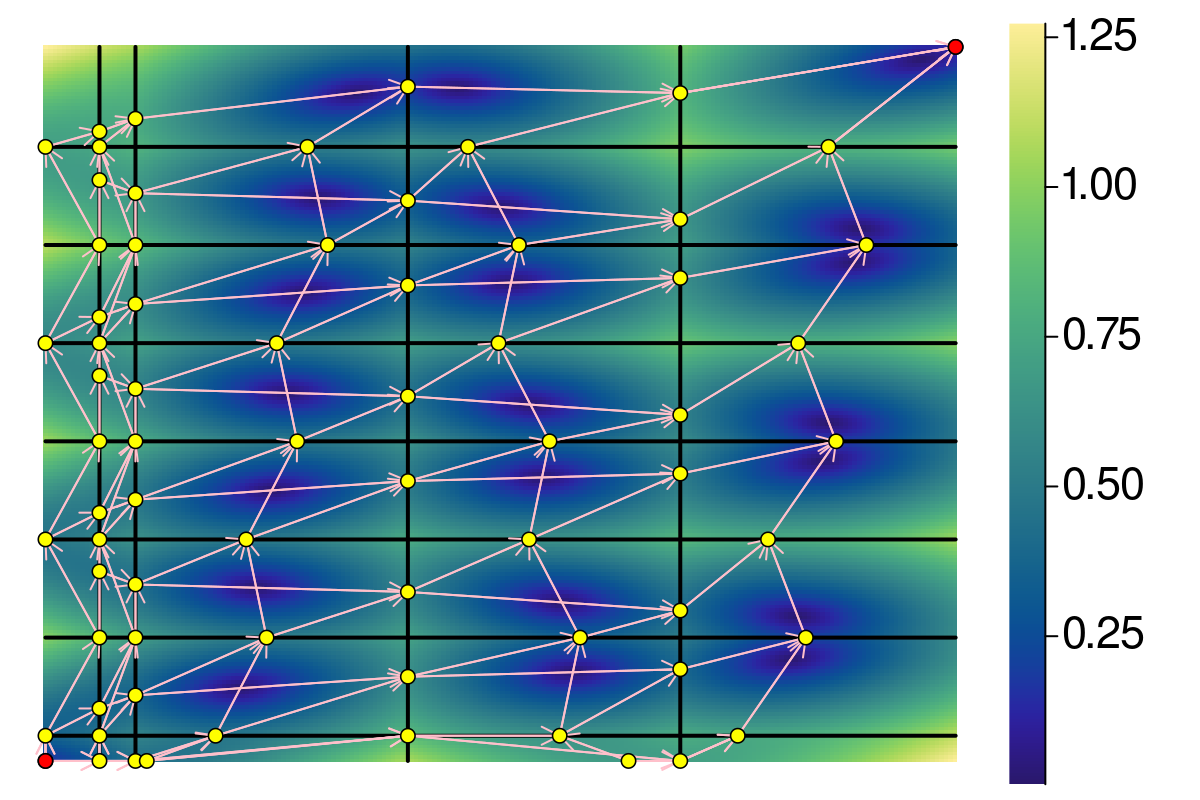
The problem: Bottleneck shortest path

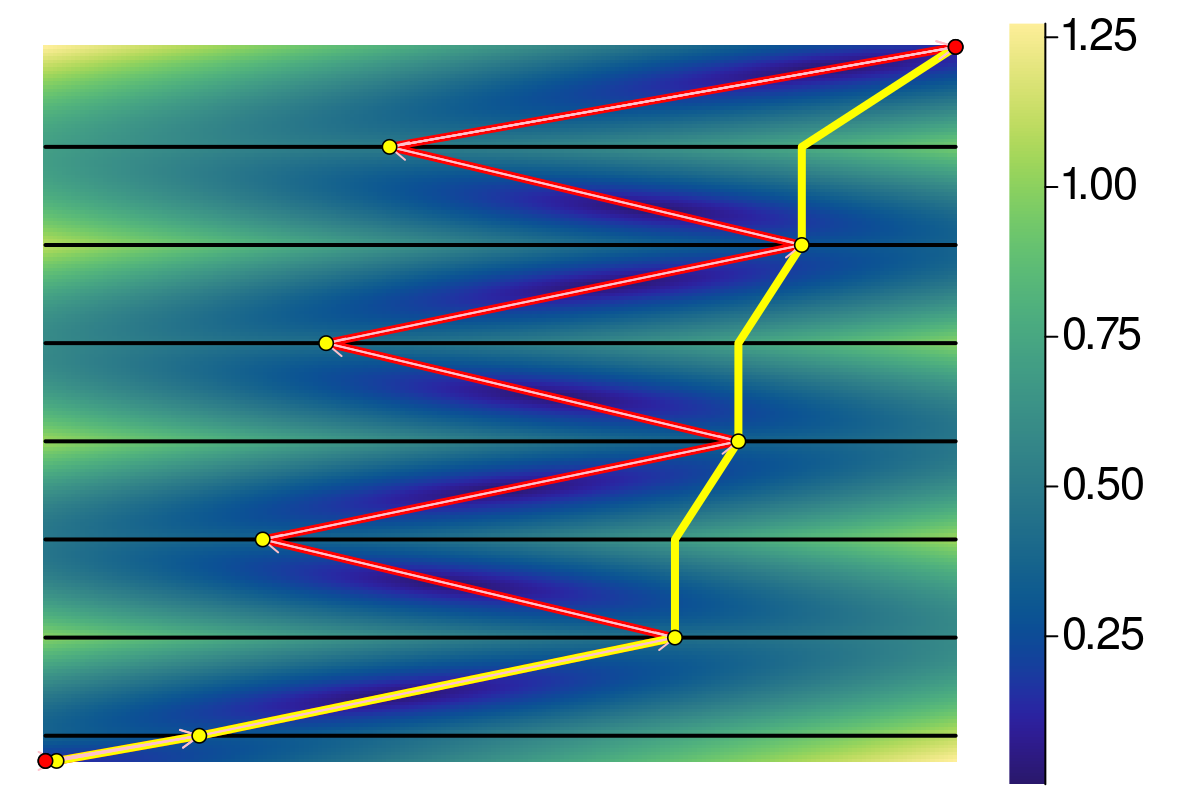
The resulting morphing

Vertex-Edge Fréchet (new¿)

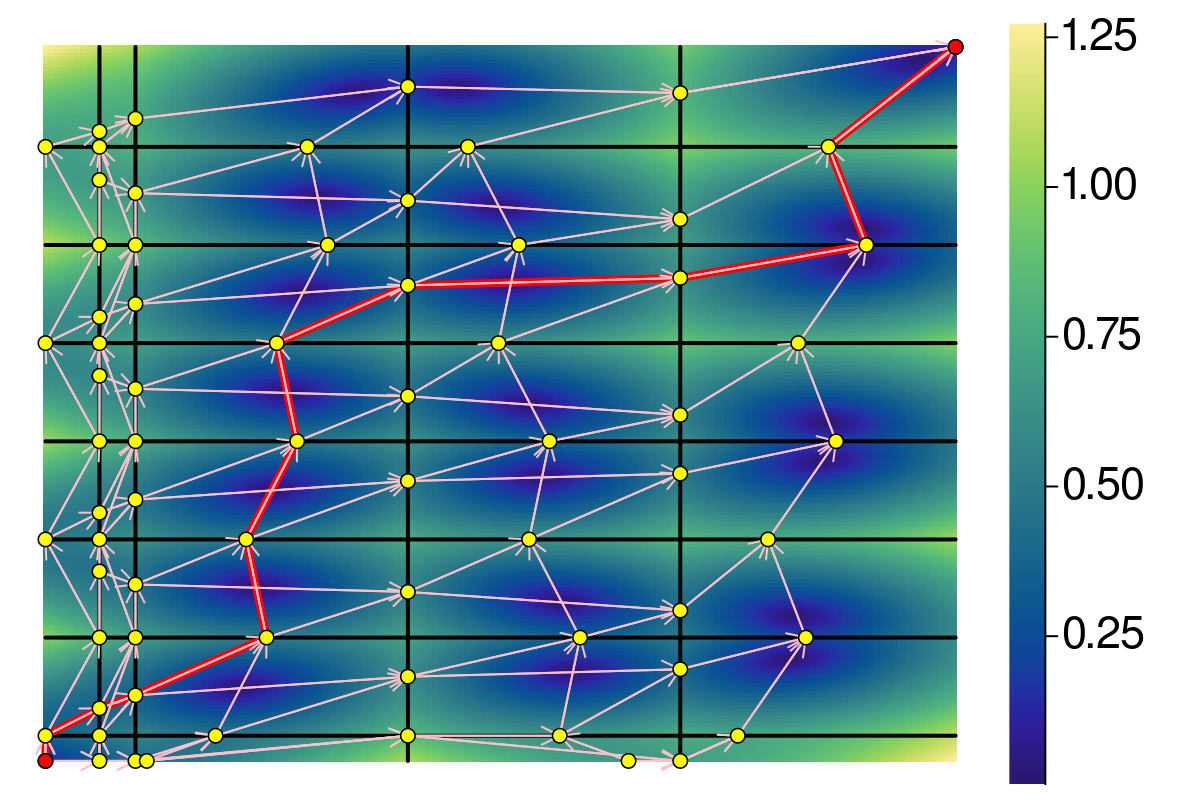
Bottleneck shortest path

Undirected graphs

• \(O(n \log n + m)\): Via MST.

• (Alt and Godau 1995) alg to compute weak Fréchet

  \(O(n^2)\).

Retractable Fréchet

Always keep leash as short as possible

\(G\): Directed graph with weights on edges

Definition: Retractable path is the bottleneck shortest path, recursively retractable when removing the bottleneck.

Retractable definition by example

Retractable Fréchet \(\implies\) better morphing

Computing Retractable Path

• Minor variant of Dijkstra/Prim:
  • From visited vertices: Take cheapest edge going out.
  • Prim algorithm for “directed” graph.
  • Stop early!
  • Faster than quadratic for “most” inputs.
  • Algorithm extremely simple (implicit grid).
• Retractable Fréchet
  • Definition due to (Buchin et al. 2019): “Locally correct”.
  • Different algorithm

Claim: \(\forall \pi, \sigma\) : \(\,\,\) \(\mathsf{d}_{\mathcal{F}}(\pi, \sigma) \geq \mathsf{d}^{ve}_{\mathcal{F}}(\pi, \sigma)\).

Non-monotonicity…

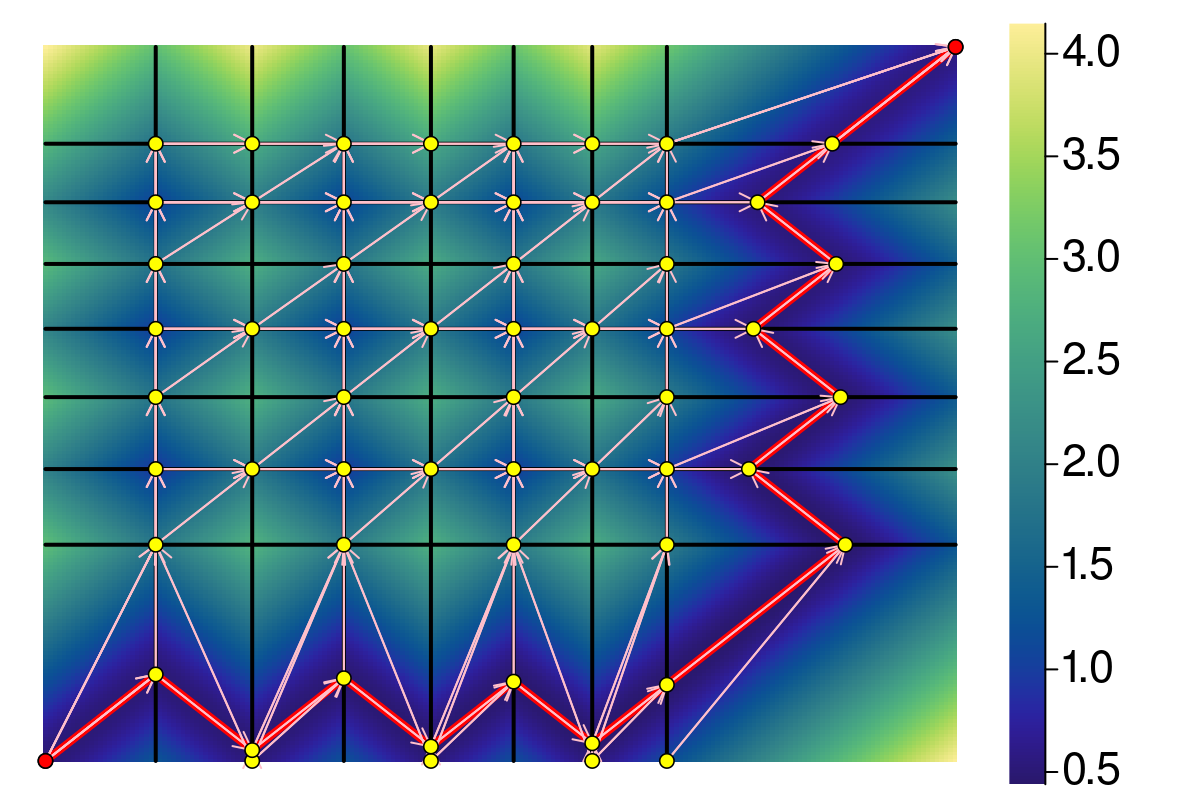
Non-monotonicity…

Brute force monotonization…

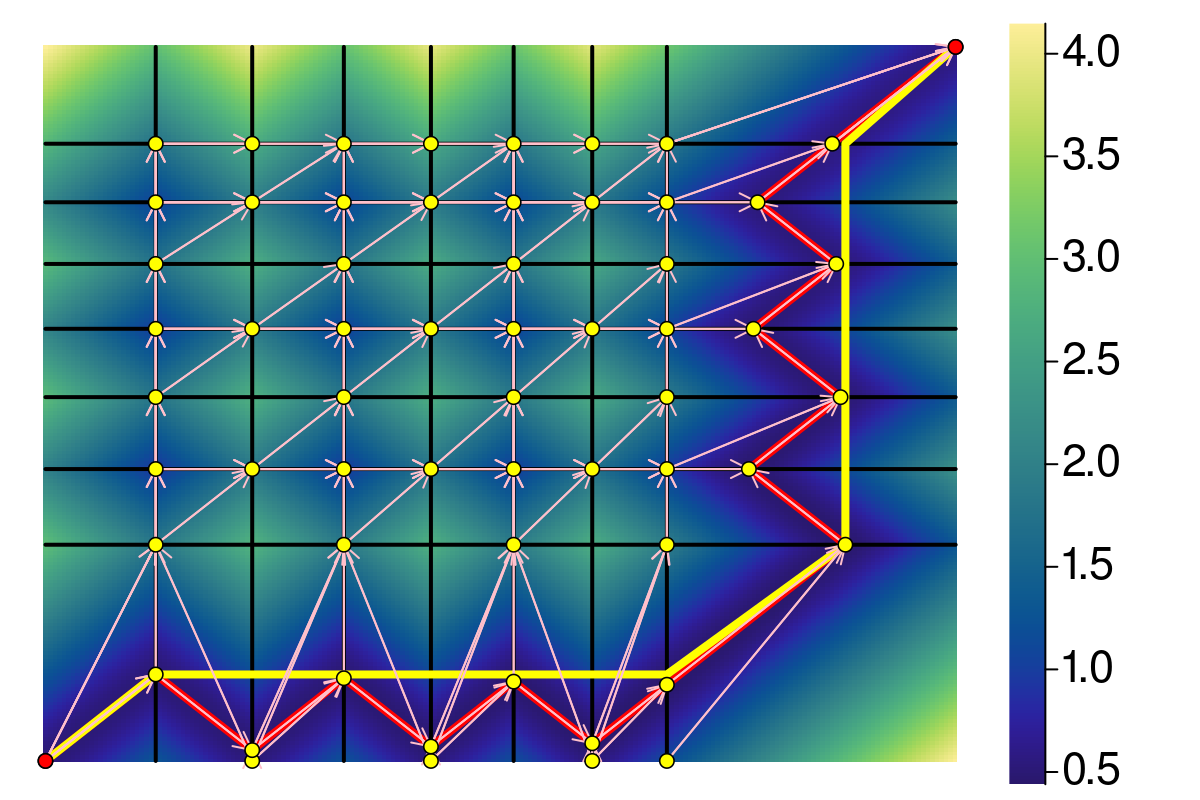
Optimal Fréchet \(\in[\mathsf{d}^{ve}_{\mathcal{F}}. \mathrm{mono}(\mathsf{d}^{ve}_{\mathcal{F}})]\).

Reduce non-monotonicity by inserting vertices

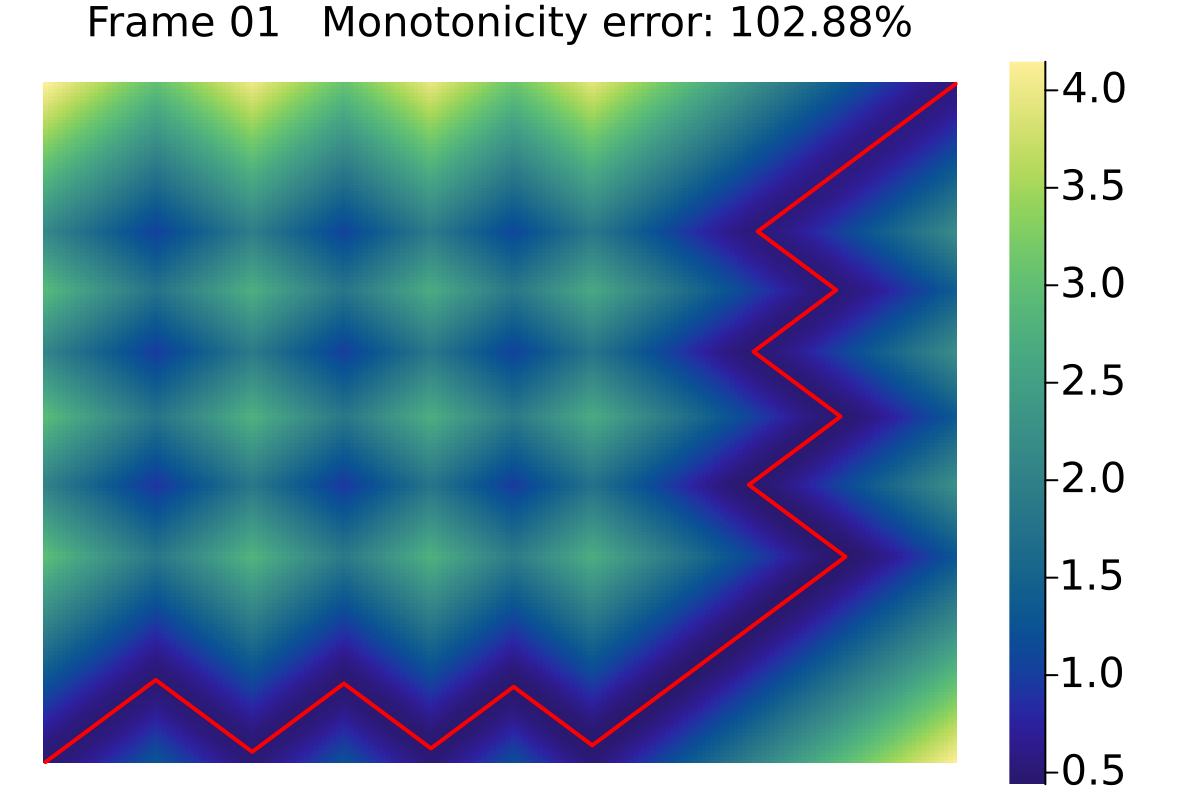
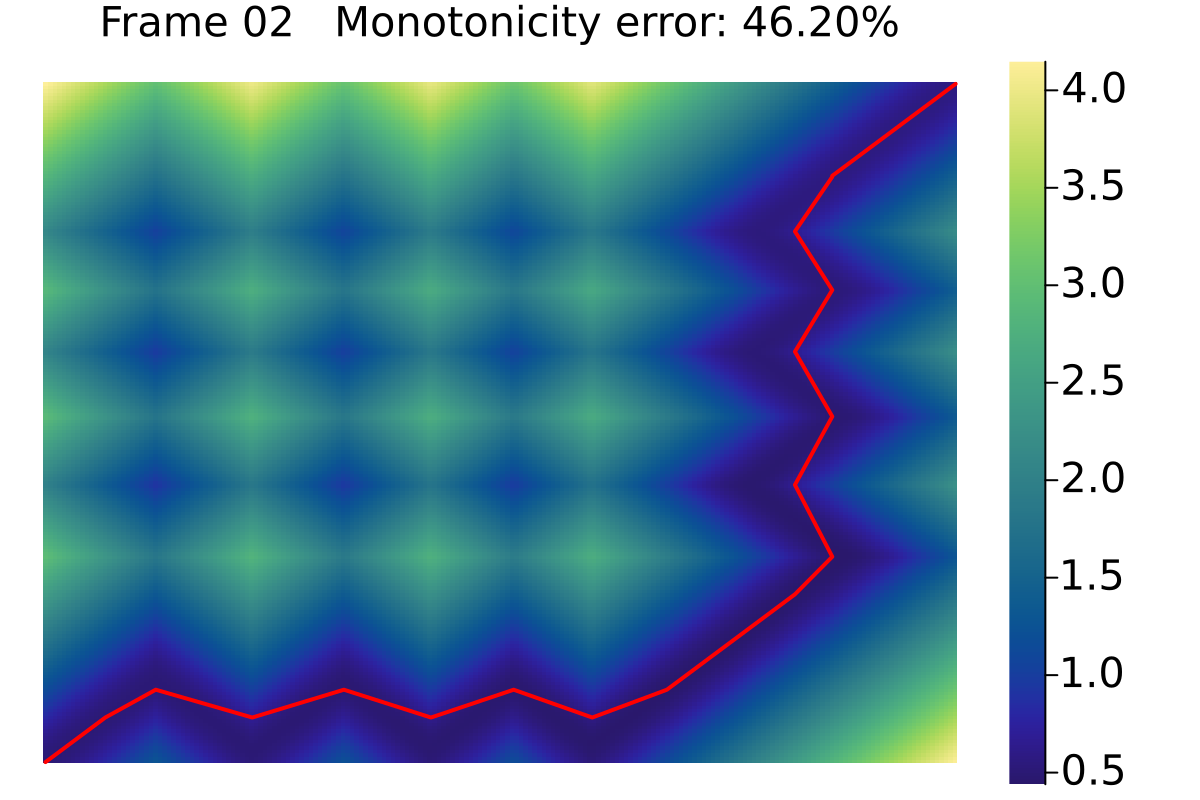
Reduce non-monotonicity by inserting vertices II

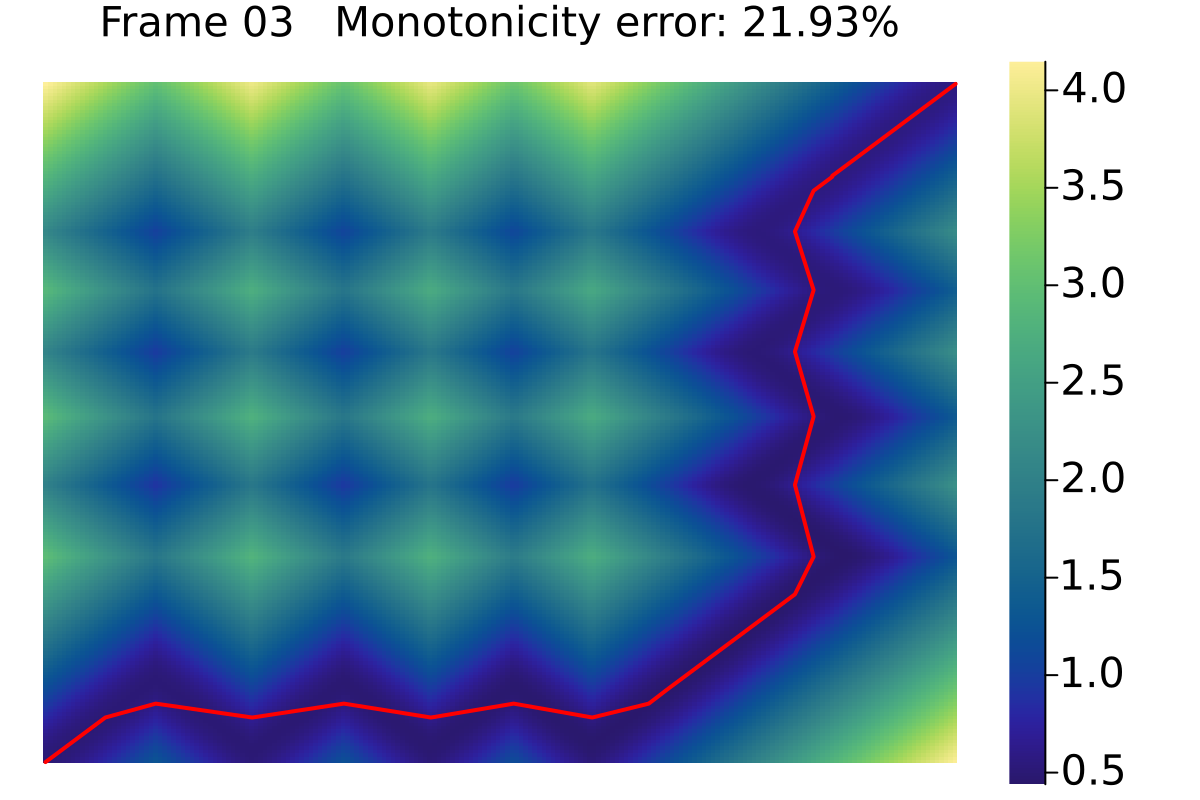
Reduce non-monotonicity by inserting vertices a few iterations later

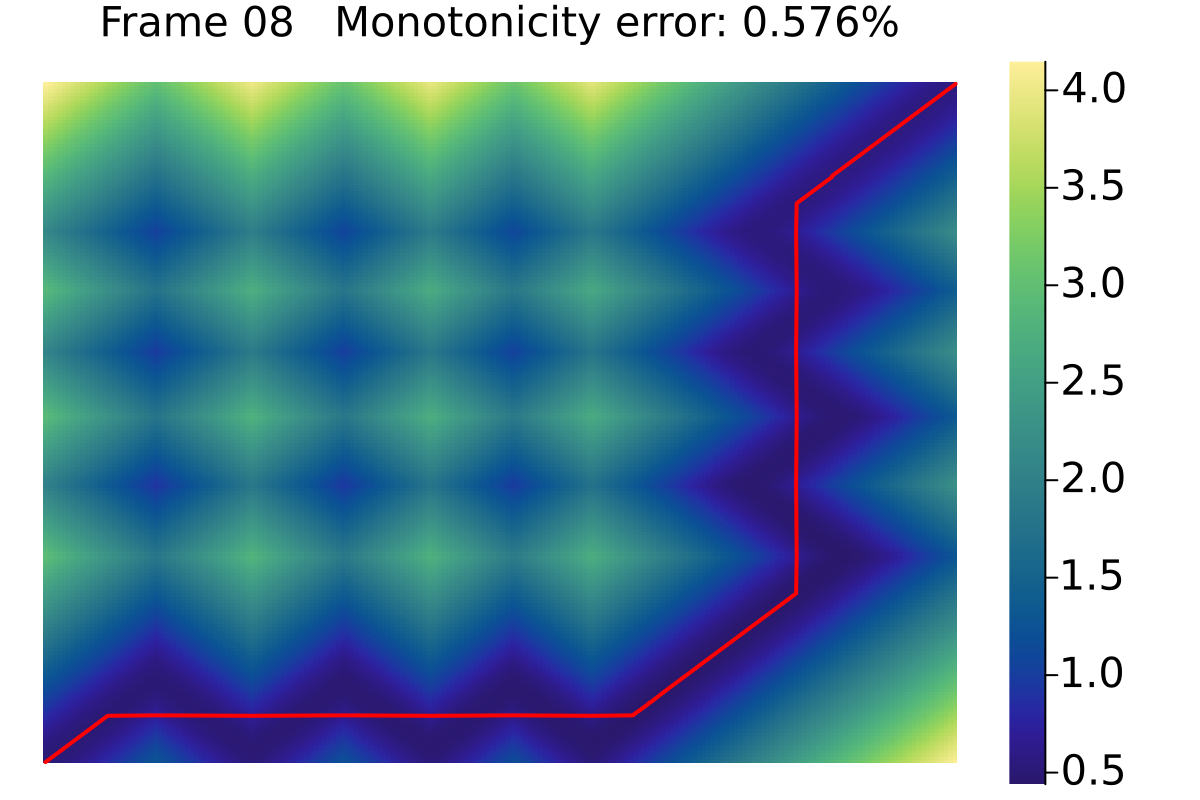
Exact \(\mathsf{d}_{\mathcal{F}}\) distance…

• While \(\mathsf{d}^{ve}_{\mathcal{F}}< \mathrm{mono}(\mathsf{d}^{ve}_{\mathcal{F}})\)
  • Refine curves
  • Recompute \(\mathsf{d}^{ve}_{\mathcal{F}}(\pi,\sigma)\)
• isolate the bottleneck…

No such thing as exact algorithms

• Floating point issues.
• Consider \(1.0001\)-approximation as exact.

The result…

• Algorithm for (exact) Retractable Fréchet

• Retractablity is important…

Approx Fréchet: segment

Comp Fréchet distance segment \(\Leftrightarrow\) curve

• \(\pi\): Polygonal curve

• \(n = |\pi|\)

• Exact: \(O(n \log n)\).

• Practice: Simple + linear time

Lemma

\(3\)-approx. \(O(n)\) time for Fréchet dist between curve and segment.

Simplification: Approx

Greedy Fréchet simplification

Approximation via simplification

• \(\pi, \sigma\): Input curves.

• \(d \leftarrow\) silly upper bound on \(\mathsf{d}_{\mathcal{F}}(\pi, \sigma)\).

• do

  • \(r \leftarrow d/10\)
  • \(\pi' \leftarrow \mathrm{simplify}(\pi, r )\).
  • \(\sigma' \leftarrow \mathrm{simplify}(\sigma, r )\).
  • \(\ell \leftarrow \mathsf{d}_{\mathcal{F}}(\pi', \sigma')\)
  • Compute morphing \(\pi\rightarrow \pi' \rightarrow \sigma' \rightarrow \sigma\)
  • If \(\frac{\ell +2r}{\ell-2r} \leq 1 + \epsilon\) \(\Rightarrow\) return approx.
  • \(d \leftarrow d/4\).

Simplification: Exact

Simplification to make speed great again

• Simplify curves (speedup).

• Do simplification preserving bottleneck.

• \(\Rightarrow\) Fast exact algorithm.

• Many details…

Morphing sensitive simplification I

Morphing sensitive simplification II

Morphing sensitive simplification III

Morphing sensitive simplification IV

Shticks and tricks

and questions

Arising from the implementation

Low quality simplification, but fast

Task: Preprocess \(\pi\) (\(10,000\)s of vertices).

Query: Given \(\delta > 0\) output curve \(\sigma\) s.t. \(\mathsf{d}_{\mathcal{F}}(\pi, \sigma) \leq \delta\).

Running time: \(O( |V(\sigma)|)\).

Output sensitive simplification…

Given \(\alpha\): Extract all vertices label \(>\alpha\).

Running time: Output sensitive.

Simplifications hierarchy/caching

• repeats many Fréchet distance queries on same curves.

• Cache simplifications curves (a hierarchy).

• use hierarchy to extract simplification quickly.

• Precompute the simplification hierarchy.

• Good idea if persistent data/task…

Implementations

Julia (Programming language)

• Python without the stupidity.

• As much typed as you want.

• built-in package manager

• Many libraries.

• Source code of everything available.

• Compiled on execution.

• Designed for multi-threaded/parallel and distributed computing

• Fun.

ACM SIGSPATIAL Cup 2017

The Fréchet distance is defined as the minimal length of a leash connecting a dog on one trajectory with its owner on a second trajectory, both never moving backwards. For this challenge, the “true” Fréchet distance shall be used, though teams are free to exploit the existing approximations including the Discrete Fréchet distance as they wish. The challenge for this year consists of finding and combining spatiotemporal indexing schemes with efficient algorithms for Range Queries in very large databases of trajectories…

C++

(Bringmann, Künnemann, and Nusser 2021): C++ implementation.

Implementation

Julia+Python package.

Experiments

(Bringmann, Künnemann, and Nusser 2021): C++ implementation.

Inputs

Julia results

Python results

Future research

Future research

• Handling noise/outliers.

• Consensus curve?

Bibliography